18.405 –
Advanced Complexity with Prof. Madhu Sudan
(Return to Petar Maymounkov's homepage.)
Related links:
Problem Sets:
Syllabus
- 2/12/04:
- Diagonalization
- Relativization,
Baker-Gill-Solovay Theorem: There are
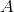 and and
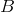 such that such that
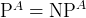 and and
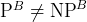 - Ladner's Theorem:
Between any two languages (one not polynomially reducible to the
other) there exist incomparable languages
- 2/20/07:
- Neciporuk's Theorem: An explicit function having a super-linear
lower-bound on formula size
- Barrington's construction of small-width Branching Programs
- 2/21/07:
- Furst-Saxe-Sipser: Parity is not in
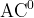 , Switching Lemma and Random
Restrictions , Switching Lemma and Random
Restrictions
- 2/26/07:
- Razborov, Method of Approximations: Replacing
deterministic gates with probabilistic polynomials
- Simplicity of
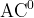 Lemma by Smolensky: Circuits in Lemma by Smolensky: Circuits in
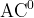 can be approximated by low-degree
polynomials on large fraction of inputs can be approximated by low-degree
polynomials on large fraction of inputs
- DeMillo-Lipton-Schwartz-Zippel Lemma of Computer Science
- Parity cannot be approximated by low-degree polynomials
- 2/28/07:
- Communication complexity (CC)
- Karchmer-Wigderson
games: Communication Complexity = Circuit depth of function
- Tiling Complexity (Yao), Tiling Lemma: Lower-bound on CC
- The rank lower bound on CC (Mehlhorn and Schmidt, STOC'82)
- 3/5/07:
- Alternation I: Alternating Machines, Space/Time/Alternation equivalences
- OPEN: Can you solve directed ST-connectivity in
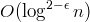 space for
space for 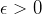 ? ?
- OPEN: Does
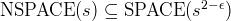 for
for
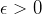 ? ?
- Fortnow's Theorem
- 3/7/07:
- Alternation II: The Polynomial Hierarchy,
classes
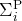 and and
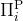
- Karp-Lipton Theorem
- 3/12/07:
- OPEN: How to generate a prime number in
![$[N,2N]$](.texinline/nxfsw8n6bcxhgw2cfm2ism7h6asq96qy.png) deterministically? deterministically?
- OPEN: Finding square
roots modulo prime deterministically (we know in RP,ZPP)
- Algebraic
Circuit Identity Testing (ACIT)
- Strong Turing-Church Hypothesis
- ZPP/RP/co-RP/BPP,
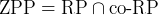
- Amplification for
(co-)RP/BPP: Success probability
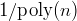 is equivalent to success
probability
is equivalent to success
probability 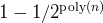
- 3/14/07:
- Amplification: Strong BPP = Weak BPP
- [Adleman]
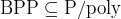 .
Implies: .
Implies:
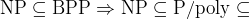 Polynomial Hierarchy collapses Polynomial Hierarchy collapses
- [Sipser, Lautemann]
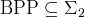
- One-way permutations
- [Valiant-Vazirani]
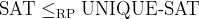 : Part I : Part I
- 3/19/07:
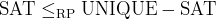
- OPEN: Can we derandomize?
- OPEN: Can we even just improve the probability of success in the reduction?

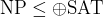
- [Toda] Parity/BP/existential/for-all operators
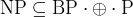 and and
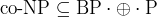
- 3/21/07:
 -operators -operators
- Classes
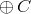 and and
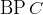 closed
under complementation closed
under complementation
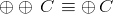 and and
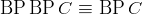 and and
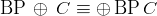
- Toda's Theorem:
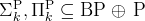 and
and
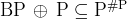
- 4/2/07:
- Interactive proofs
- [Babai-Moran] Arthur-Merlin Proofs
- [Goldreich-Micali-Wigderson] GRAPH NON-ISOMORPHISM by IP[2]
- Private coins = public coins
- One-sided error = two-sided error
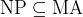 and and
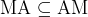 and and
![$\\text{BPP}\\subseteq \\text{MA}=\\text{AMAMAM ... } \\subseteq
\\text{IP}[\\text{poly}]= \\text{PSPACE}$](.texinline/8ejypvg8cc3cpjcfm8rfbvd7b2y9us9z.png) . Last equality by
[Lund-Fortnow-Karloff-Nissan, Shamir] . Last equality by
[Lund-Fortnow-Karloff-Nissan, Shamir]
- Private coins and 2-sided error = public coins and 1-sided error
- PERMANENT is random-self reducible
|
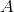 and
and
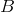 such that
such that
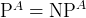 and
and
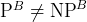
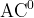 , Switching Lemma and Random
Restrictions
, Switching Lemma and Random
Restrictions 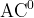 Lemma by Smolensky: Circuits in
Lemma by Smolensky: Circuits in
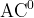 can be approximated by low-degree
polynomials on large fraction of inputs
can be approximated by low-degree
polynomials on large fraction of inputs
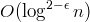 space for
space for 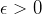 ?
?
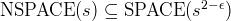 for
for
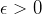 ?
?
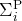 and
and
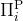
![$[N,2N]$](.texinline/nxfsw8n6bcxhgw2cfm2ism7h6asq96qy.png) deterministically?
deterministically?
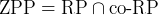
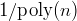 is equivalent to success
probability
is equivalent to success
probability 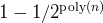
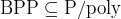 .
Implies:
.
Implies:
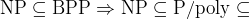 Polynomial Hierarchy collapses
Polynomial Hierarchy collapses
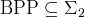
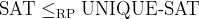 : Part I
: Part I
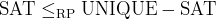

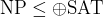
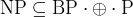 and
and
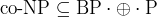
 -operators
-operators
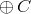 and
and
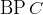 closed
under complementation
closed
under complementation
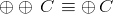 and
and
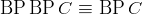 and
and
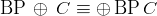
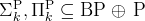 and
and
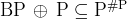
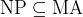 and
and
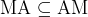 and
and
![$\\text{BPP}\\subseteq \\text{MA}=\\text{AMAMAM ... } \\subseteq
\\text{IP}[\\text{poly}]= \\text{PSPACE}$](.texinline/8ejypvg8cc3cpjcfm8rfbvd7b2y9us9z.png) . Last equality by
[Lund-Fortnow-Karloff-Nissan, Shamir]
. Last equality by
[Lund-Fortnow-Karloff-Nissan, Shamir]