Sparsest-cut and negative-type metricsRecall that the sparsest-cut value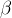 is
defined as: is
defined as:
Arora-Rao-Vazirani: Key TheoremAssume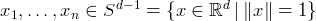 are
such that for all are
such that for all ![$i,j,k\\in[n]$](.texinline/2p2xsti9iueqwfxiydmur4rx5w89jvis.png) it holds that
it holds that 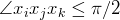 ,
as well as: ,
as well as:
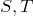 such that: such that:

|
Sparsest-cut and negative-type metricsRecall that the sparsest-cut value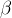 is
defined as: is
defined as:
Arora-Rao-Vazirani: Key TheoremAssume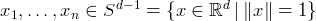 are
such that for all are
such that for all ![$i,j,k\\in[n]$](.texinline/2p2xsti9iueqwfxiydmur4rx5w89jvis.png) it holds that
it holds that 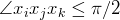 ,
as well as: ,
as well as:
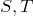 such that: such that:

|